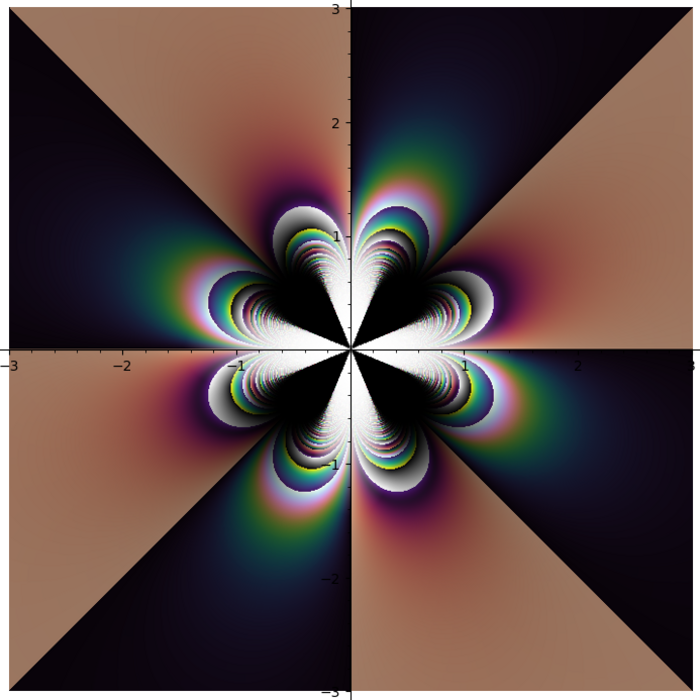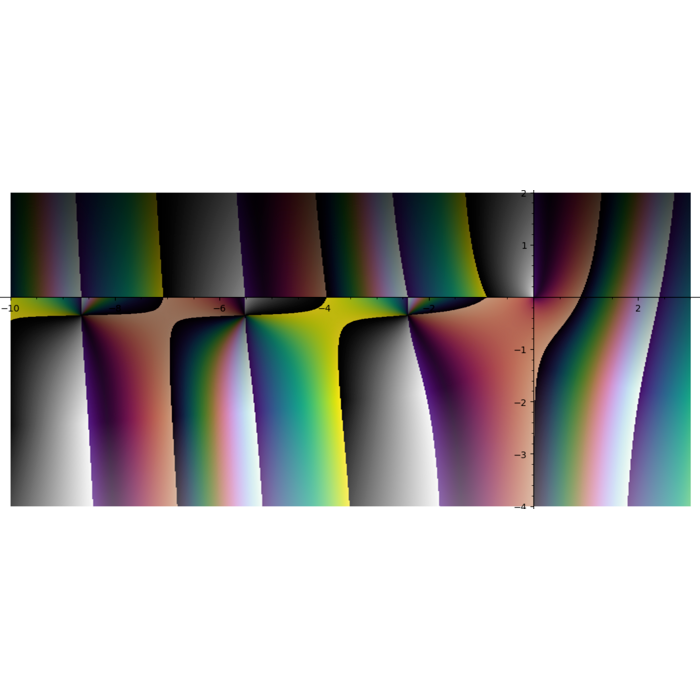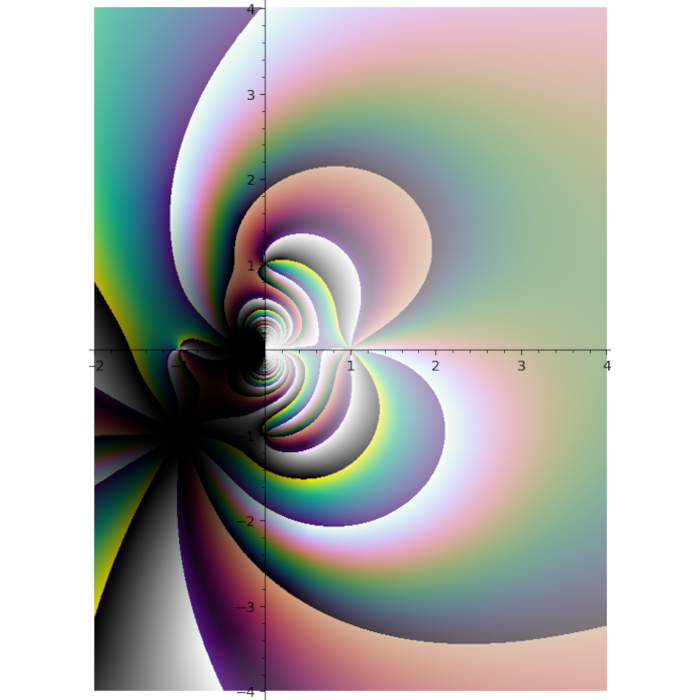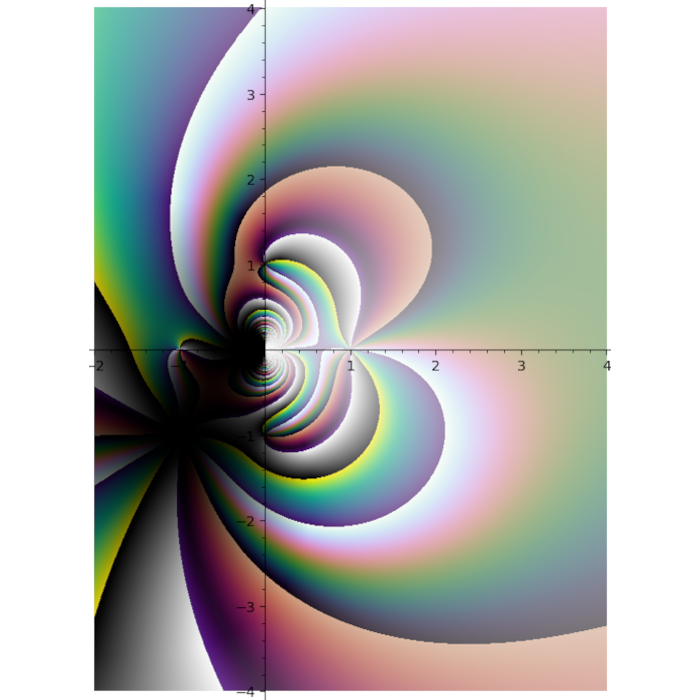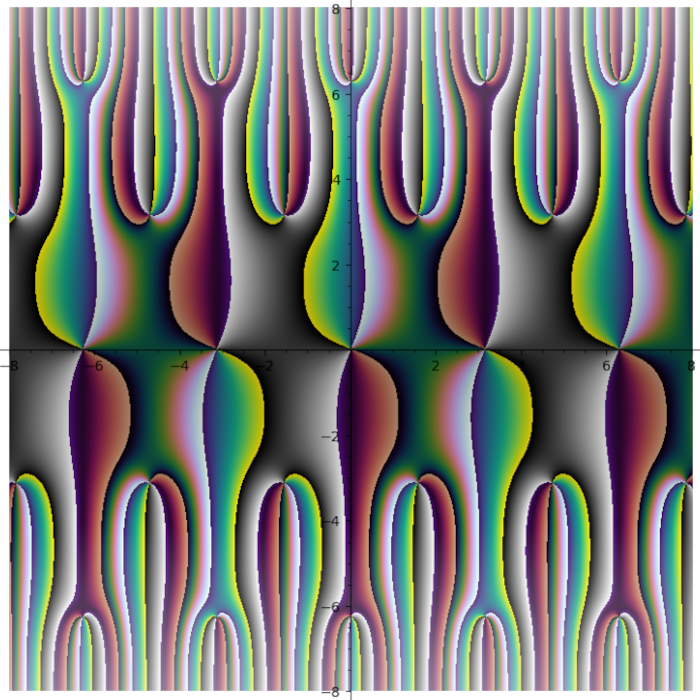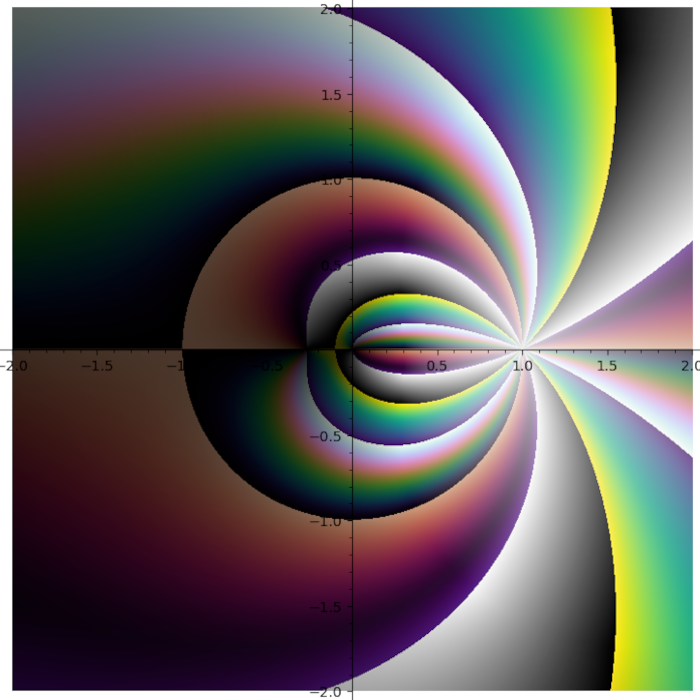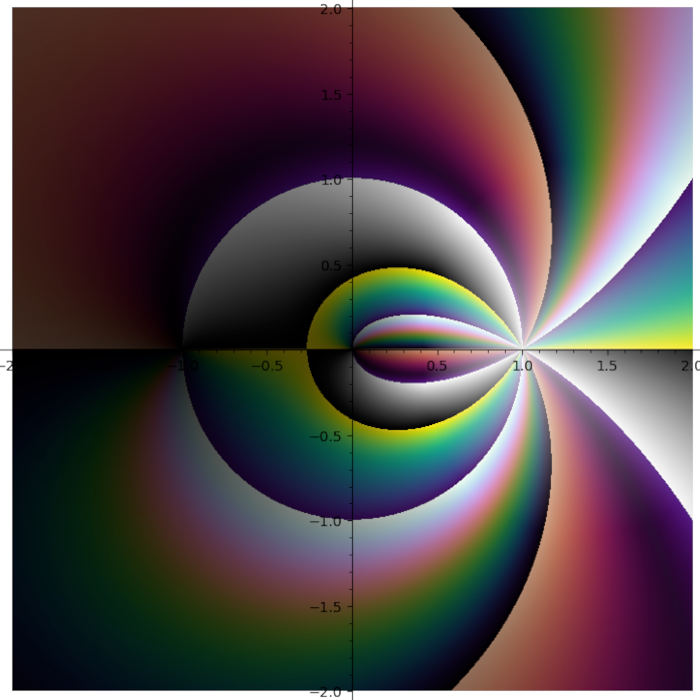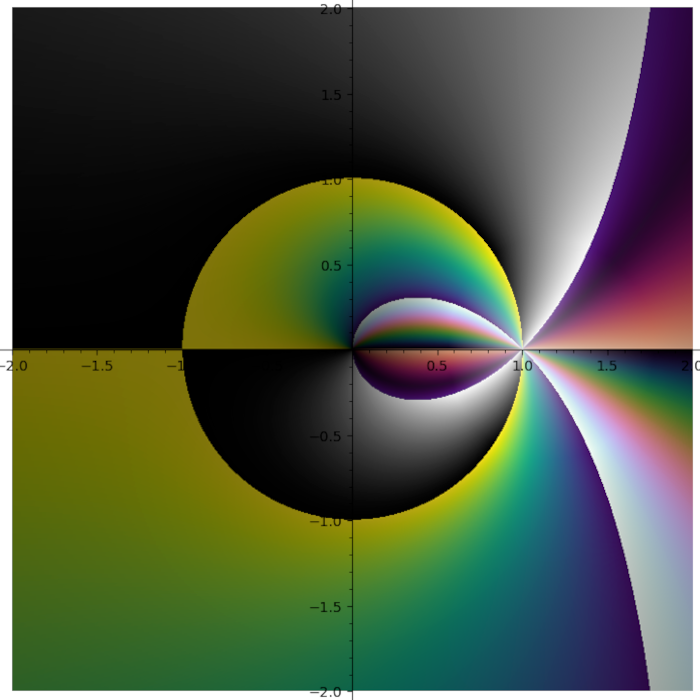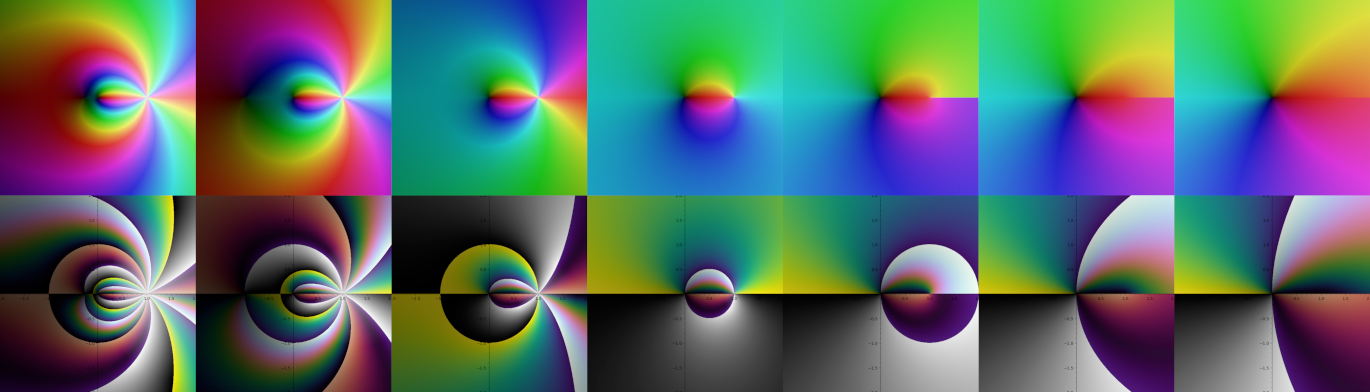
Different polylogarithm functions in the complex plane
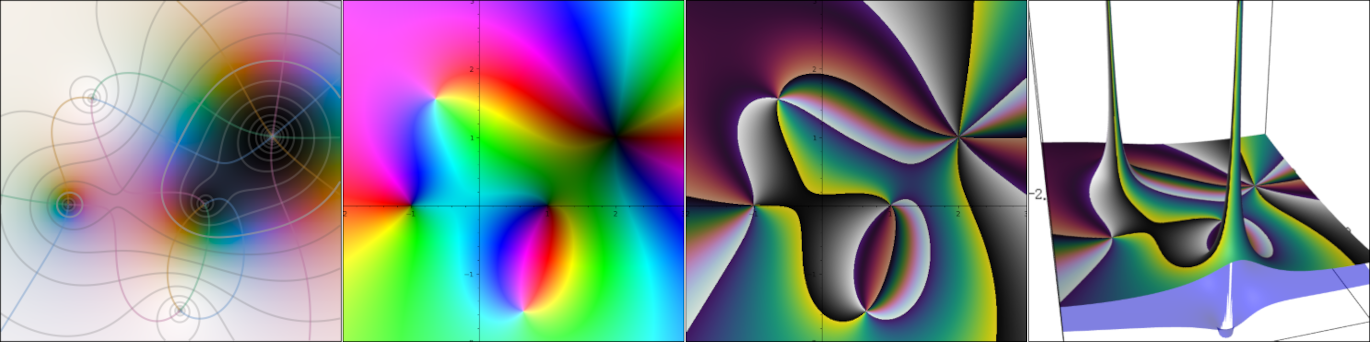
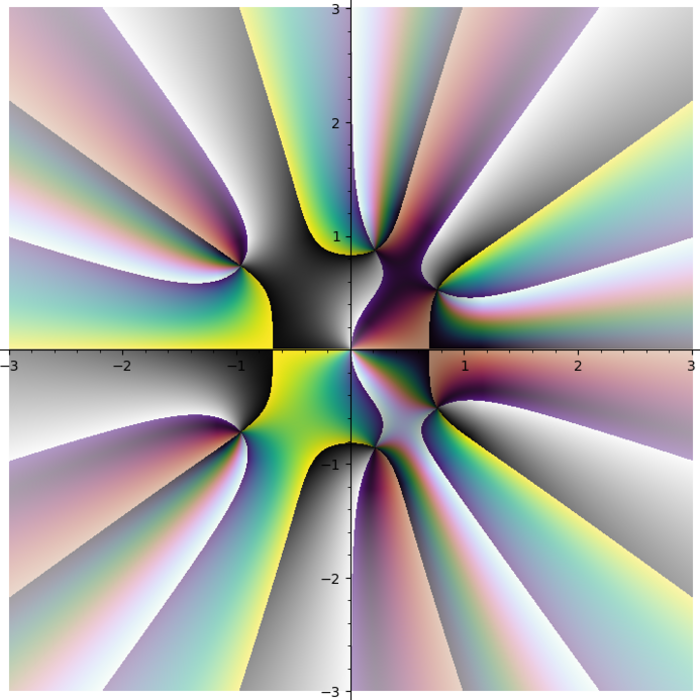
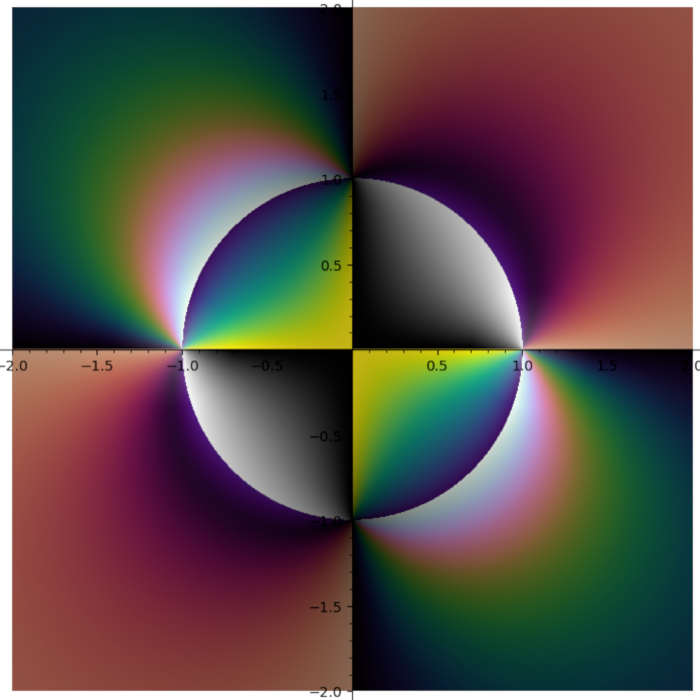
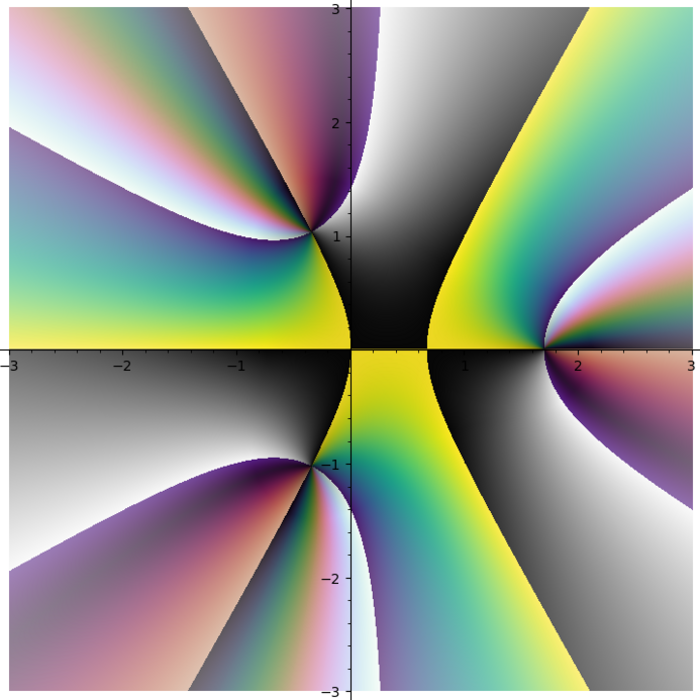
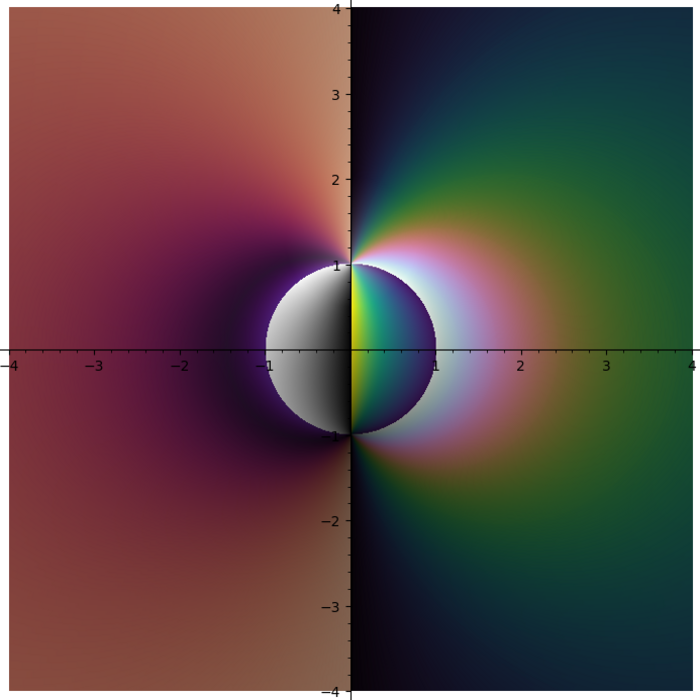
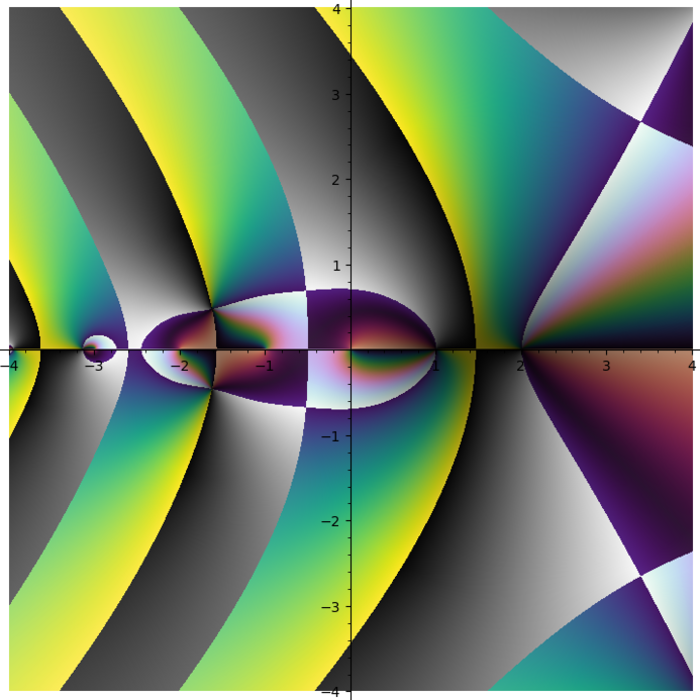
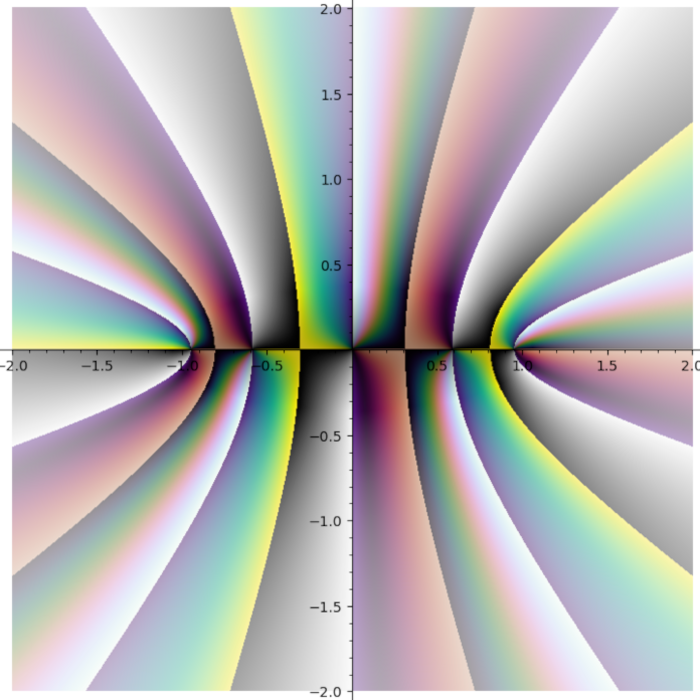
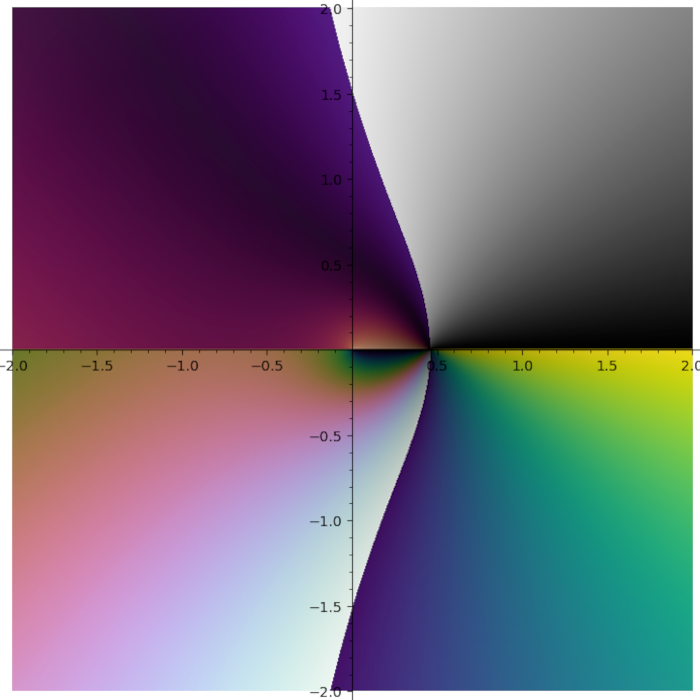
Domain coloring plot of the function \(f(x) = \frac{{\left(x^{2} - 1\right)} {\left(x - i - 2\right)}^{2}}{x^{2} + 2 i + 2}\)
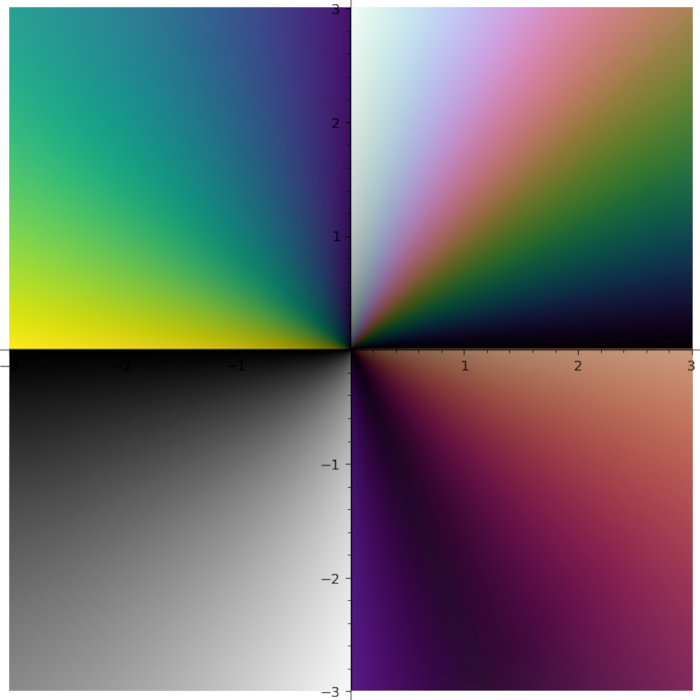
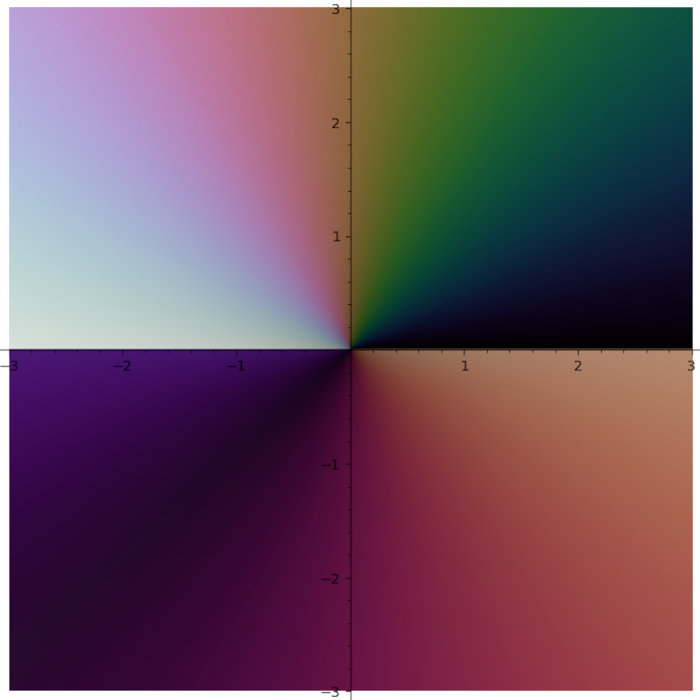
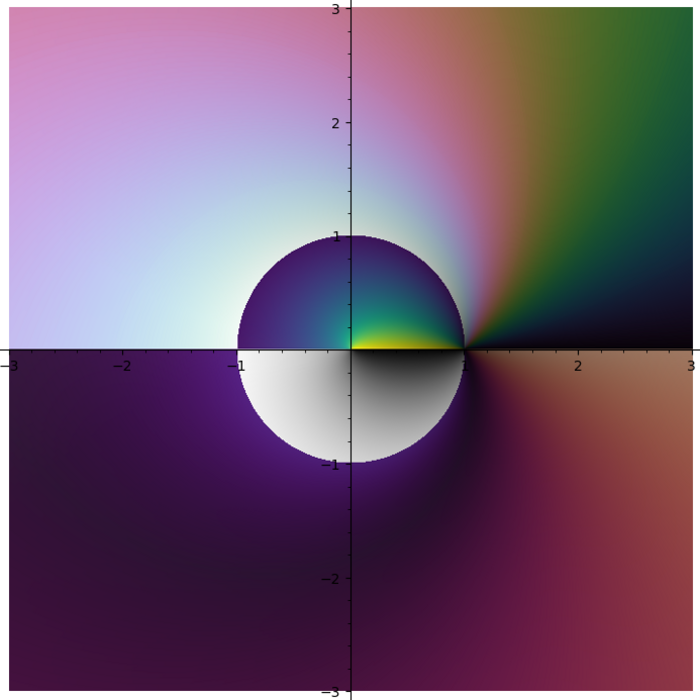
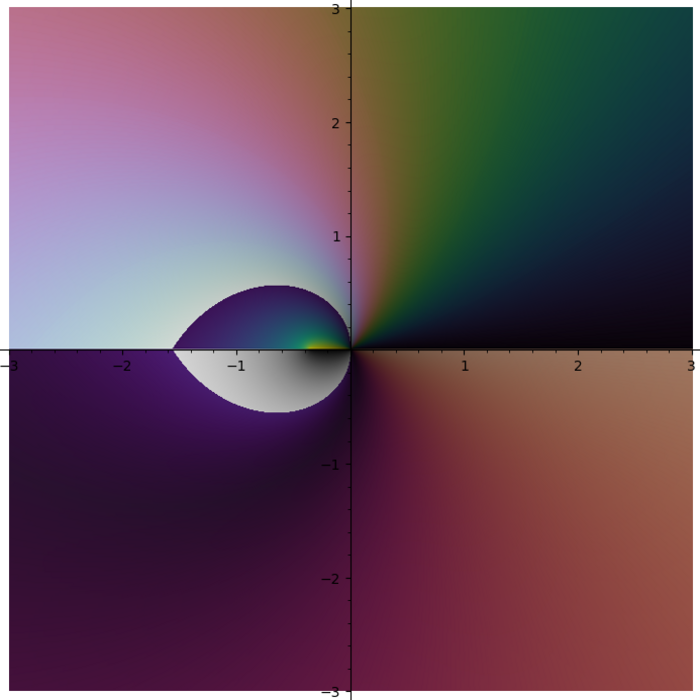
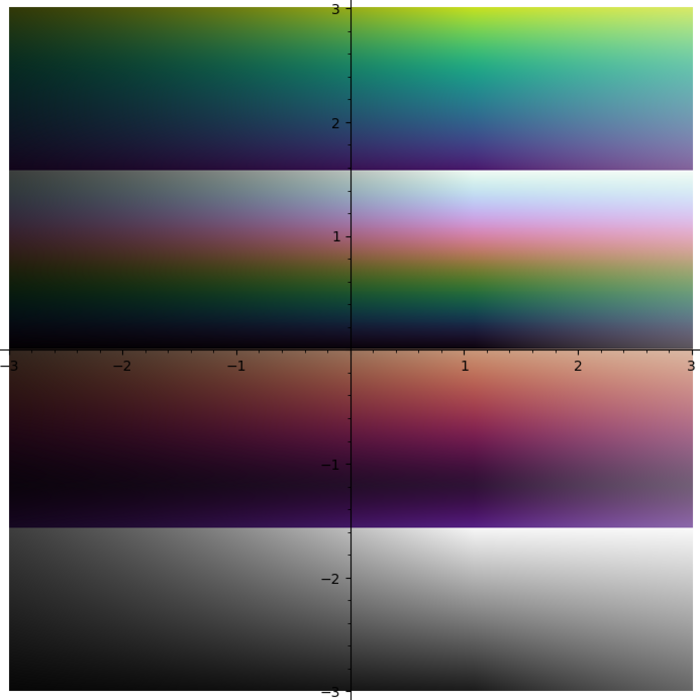
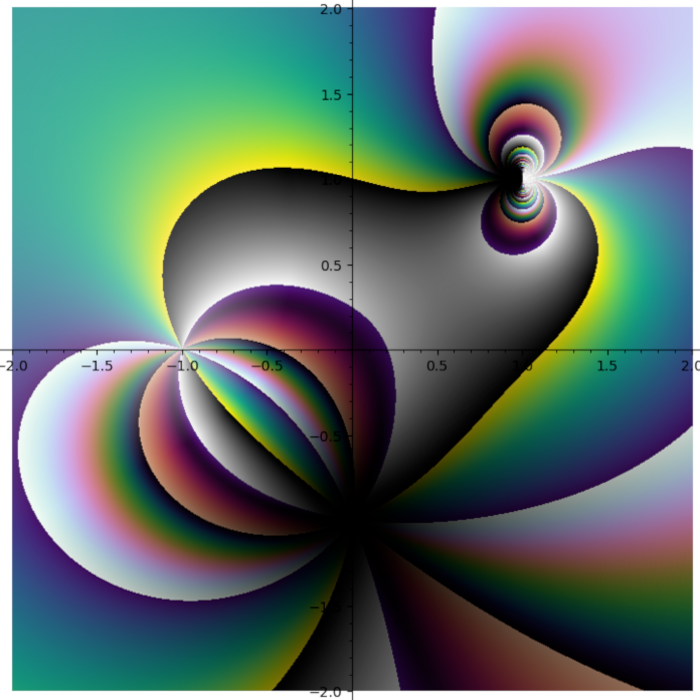
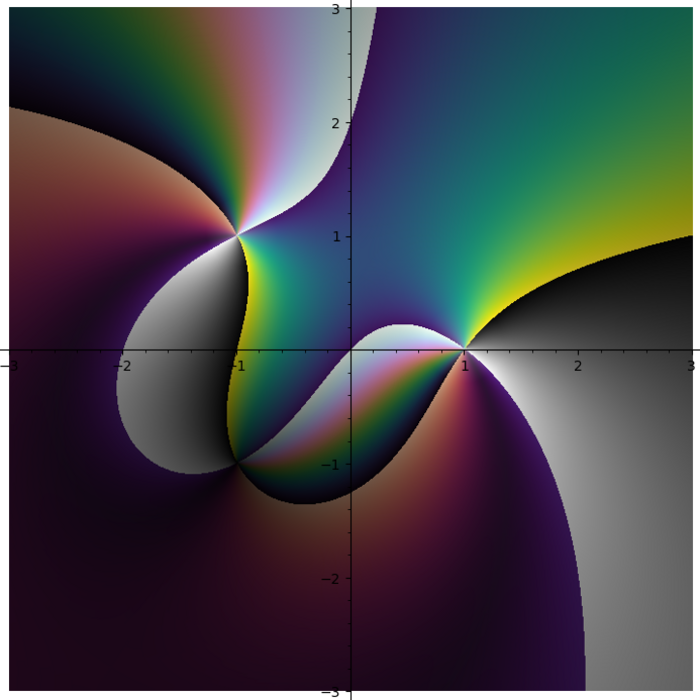
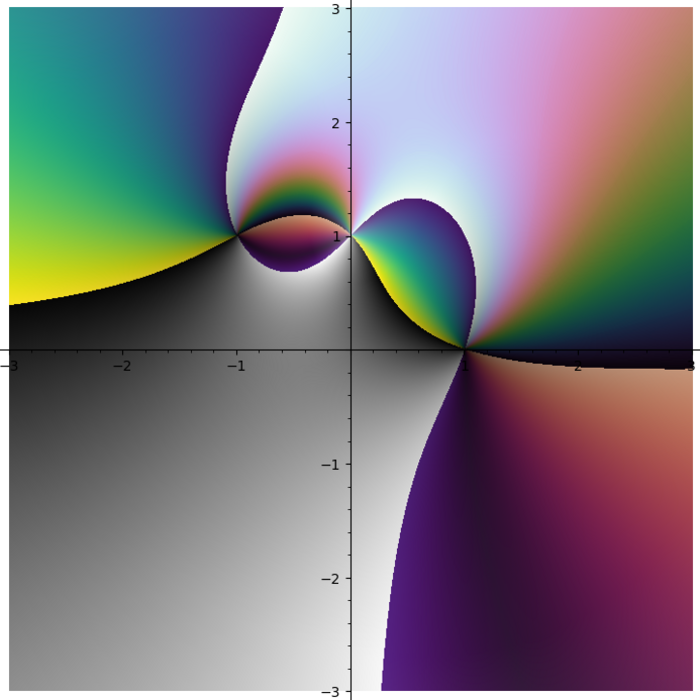
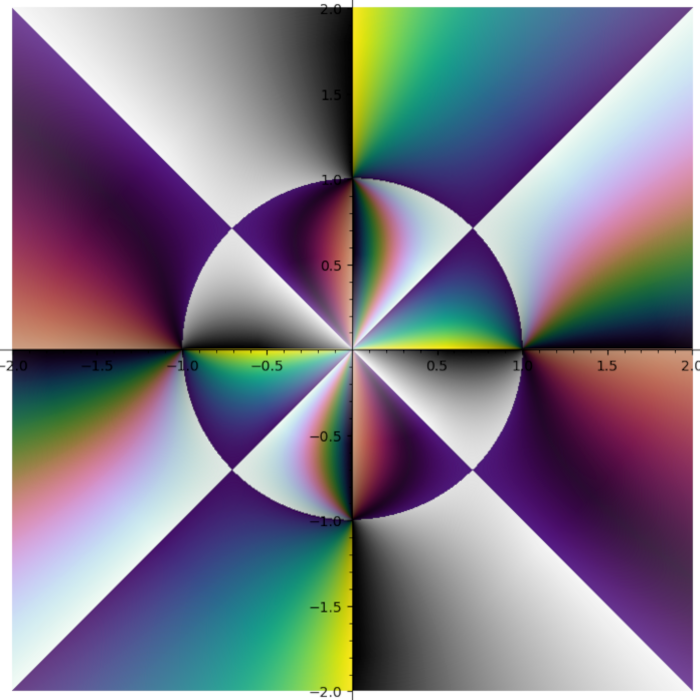
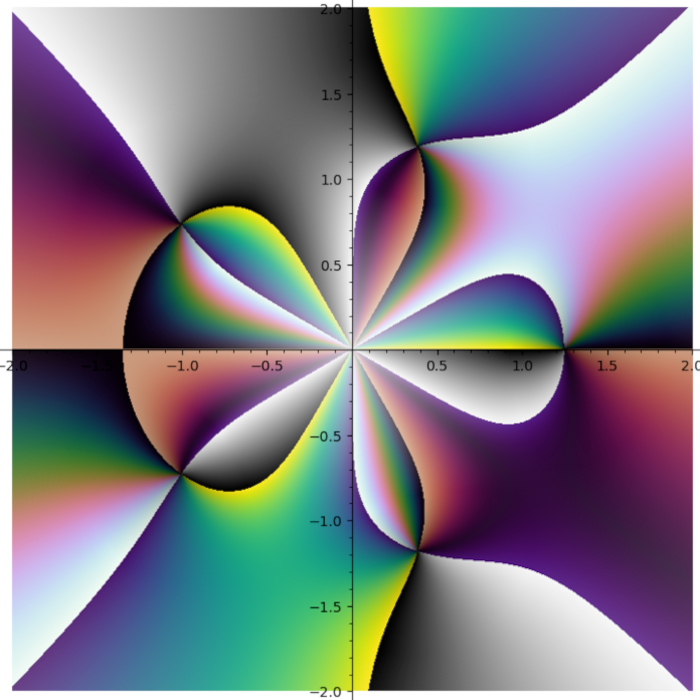
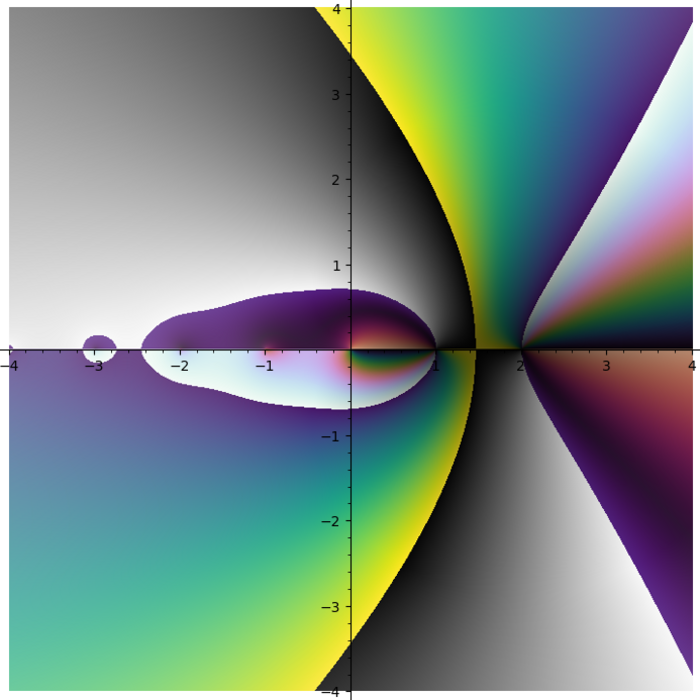
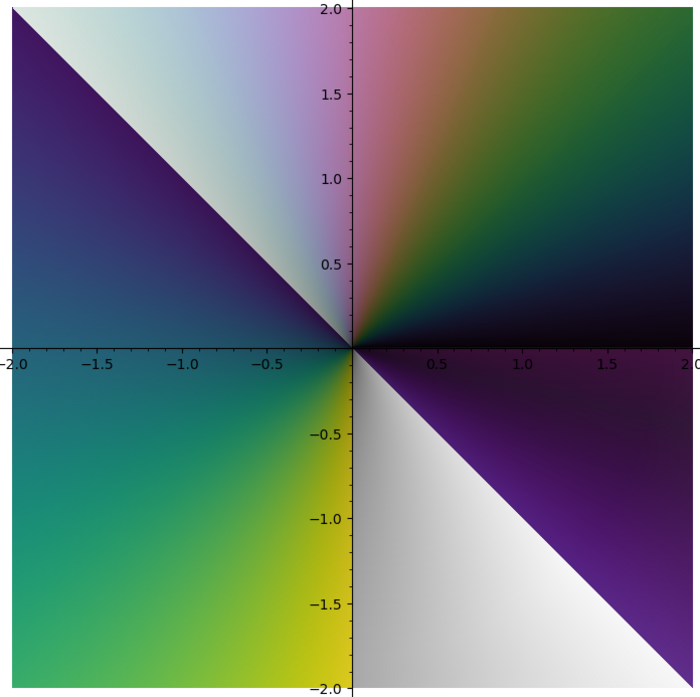
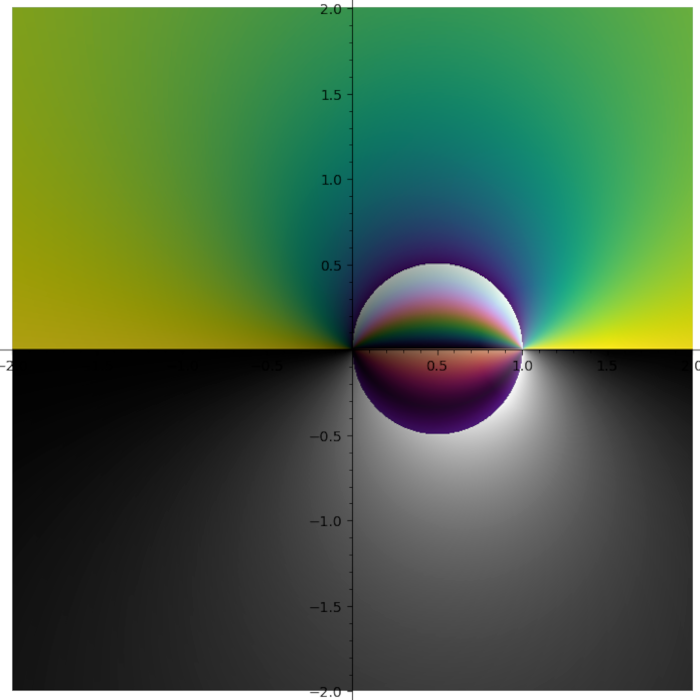
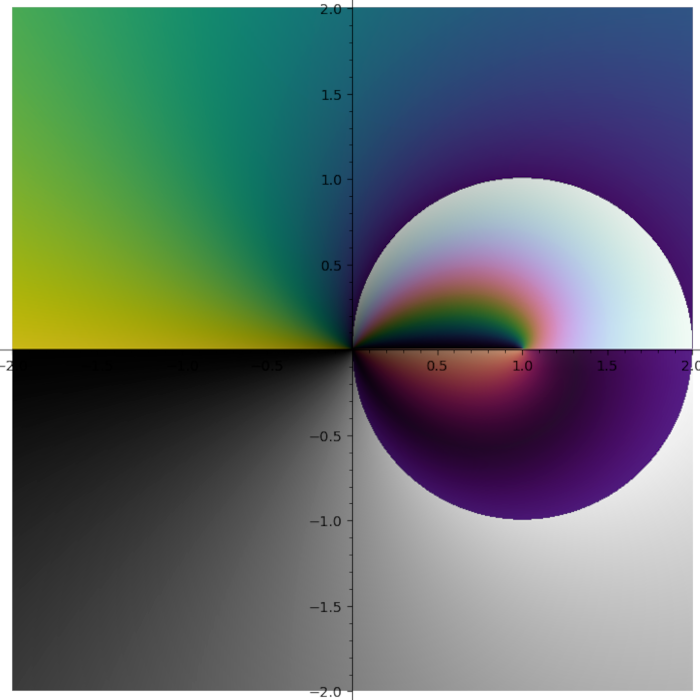
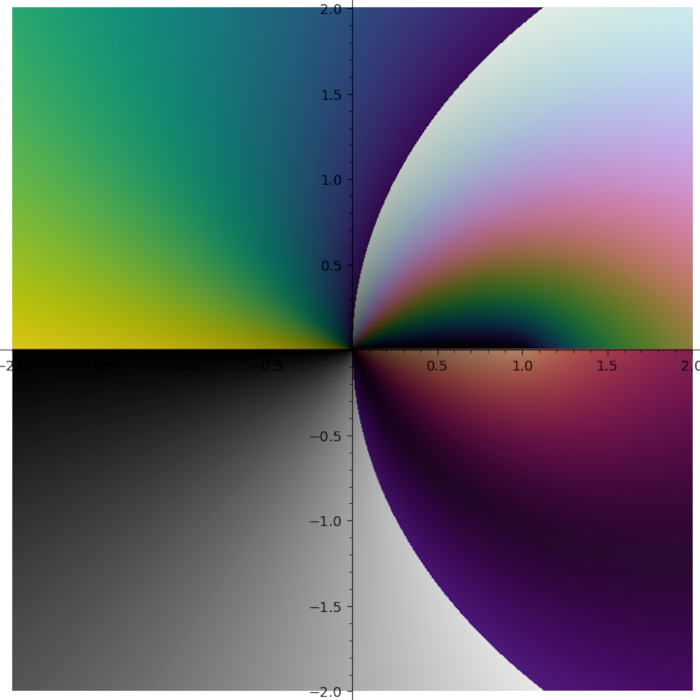
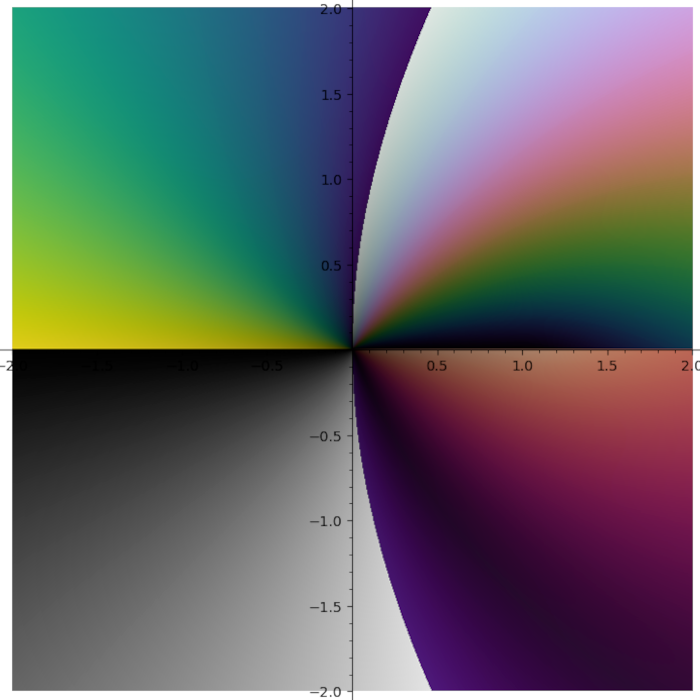
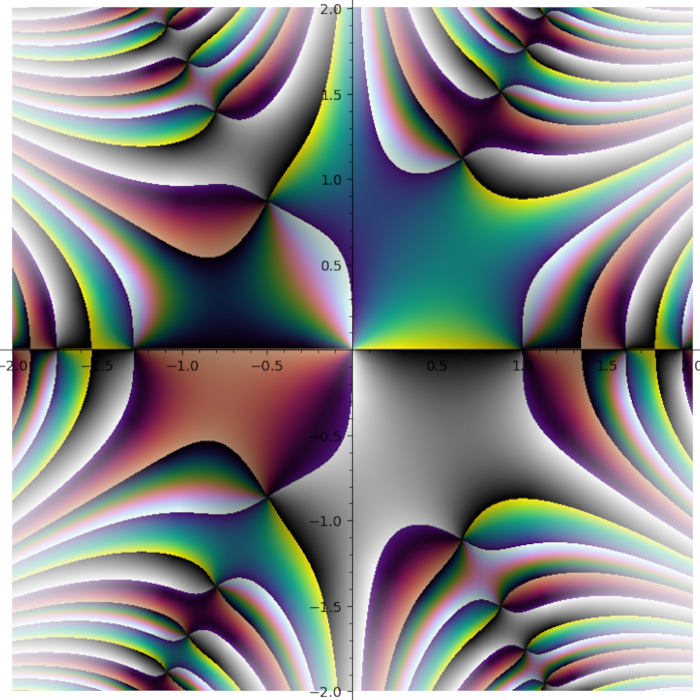
I do not like rainbow colormap. Too bright. Too colorful. And it does not tell you what quadrant you are in. I need colormap with four contrast borders and there is no such colormap in Matplotlib. So I smashed together my four favourite colormaps (gray + half of the twilight [1] + cubehelix + viridis) into one:

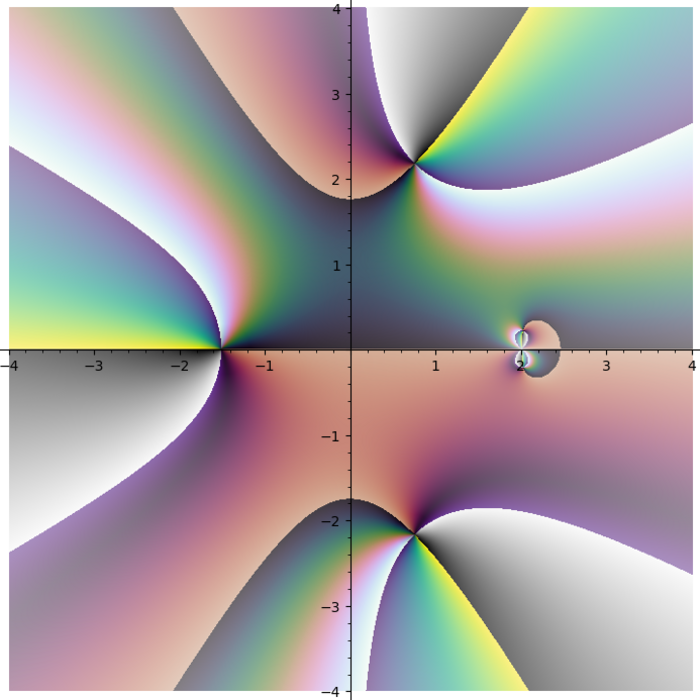
Now I can finally complex_plot and plot3d the way I wanted.
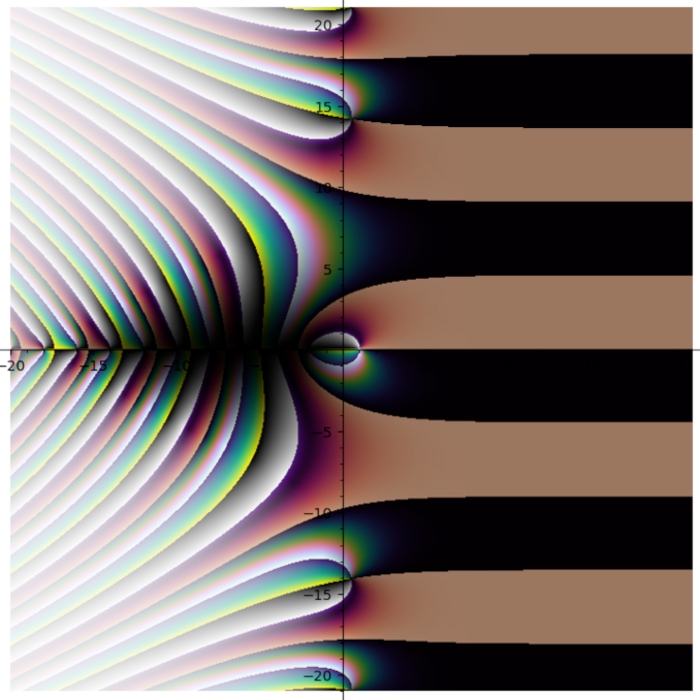
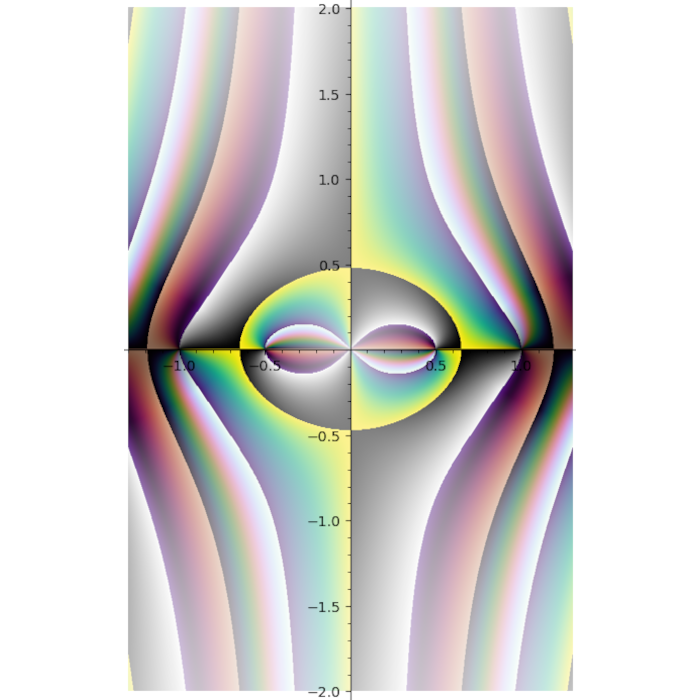
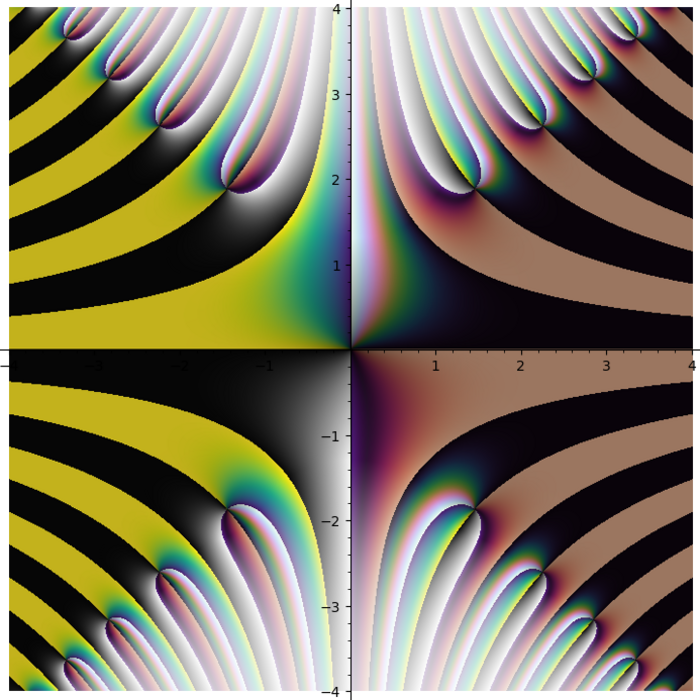
Turns out some plots have distinct stripes. You just can not see them with other colormaps.
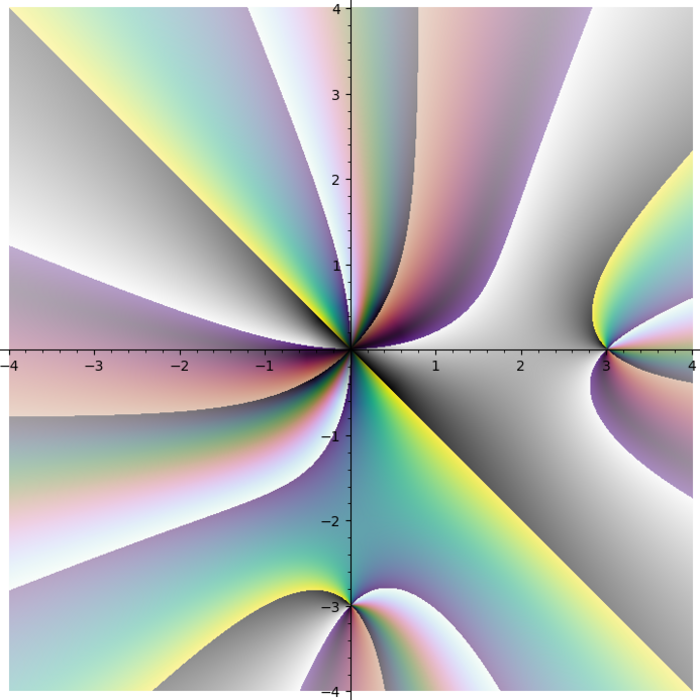
Turns out putting cubehelix in the first quadrant was a great idea.
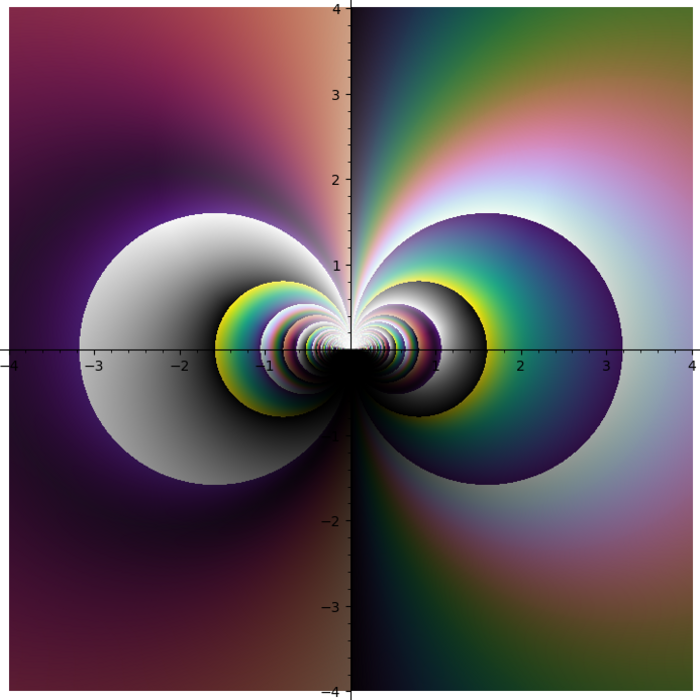
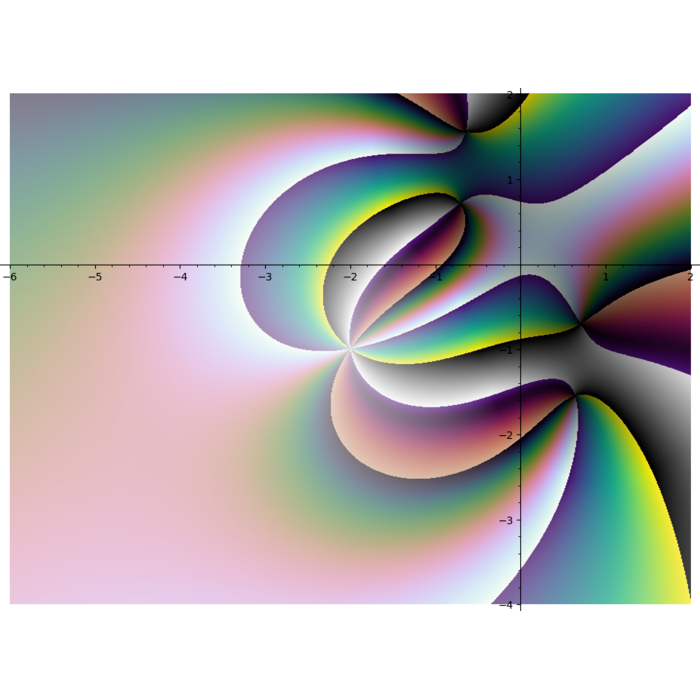
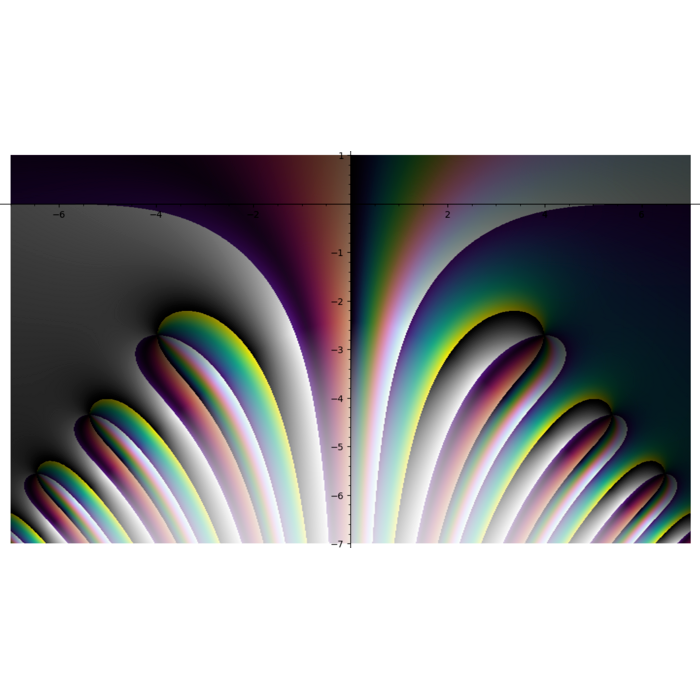
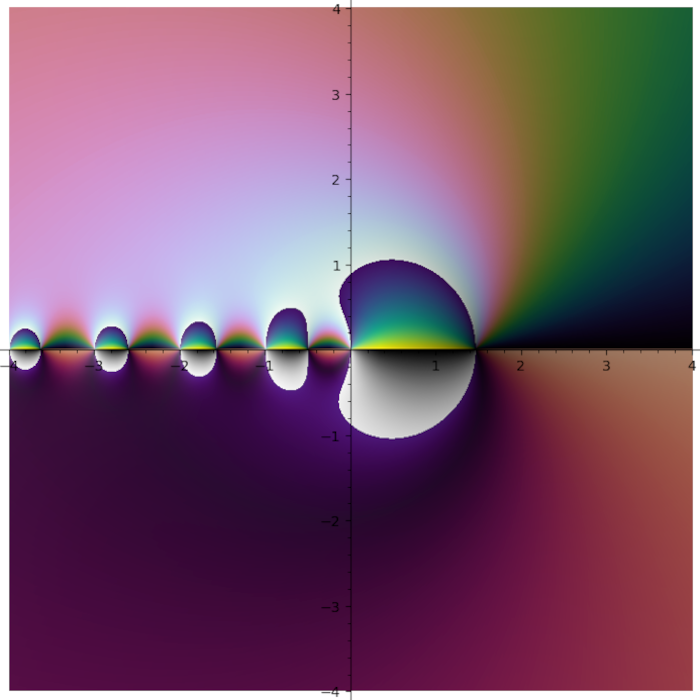
I feel like I see things that nobody else sees. Like this thing for \(f(z) = \frac{e^{\left(-z\right)}}{z^{3}}\)
I thought it would be nice to show you all this stuff, you might find it beautiful.
The rest of this page is just the links to Three.js-based memory consuming 3D plots with corresponding 2D plots.
You can use up and down arrow keys to move between plots.
|
24 Mb on disk, 340 Mb in RAM |
|
35 Mb on disk, 480 Mb in RAM |
|
13 Mb on disk, 190 Mb in RAM |
|
55 Mb on disk, 740 Mb in RAM |
|
\(f(z) = \operatorname{W}({z})\) 55 Mb on disk, 740 Mb in RAM |
|
21 Mb on disk, 300 Mb in RAM |
|
\(f(z) = z^{5} + z + \frac{1}{z} - 1\) 20 Mb on disk, 280 Mb in RAM |
|
51 Mb on disk, 690 Mb in RAM |
|
\(f(z) = \Gamma\left(z\right)\) 71 Mb on disk, 930 Mb in RAM |
|
\(f(z) = {\left(z + 3 i\right)} {\left(z - 3\right)} z^{2}\) 29 Mb on disk, 400 Mb in RAM |
|
\(f(z) = \frac{z^{2} + 1}{z^{2} - 1}\) 33 Mb on disk, 450 Mb in RAM |
|
32 Mb on disk, 470 Mb in RAM |
|
\(f(z) = e^{\left(\frac{5 i}{z}\right)}\) 56 Mb on disk, 740 Mb in RAM |
|
\(f(z) = \frac{e^{\left(-z\right)}}{z^{3}}\) 31 Mb on disk, 420 Mb in RAM |
|
21 Mb on disk, 300 Mb in RAM |
|
\(f(z) = -\frac{z + i + 1}{z^{2} - i \, z + i - 1}\) 34 Mb on disk, 470 Mb in RAM |
|
\(f(z) = \frac{z^{2} - i \, z + i - 1}{z - i}\) 46 Mb on disk, 620 Mb in RAM |
|
\(f(z) = \frac{\sin\left(2 \, \pi z\right)}{z^{3}}\) 30 Mb on disk, 440 Mb in RAM |
|
\(f(z) = \frac{z^{4} - 1}{z^{2}}\) 35 Mb on disk, 520 Mb in RAM |
|
\(f(z) = \frac{z + i}{z - i}\) 35 Mb on disk, 480 Mb in RAM |
|
\(f(z) = \frac{z^{5} - 3}{z^{3}}\) 33 Mb on disk, 450 Mb in RAM |
|
\(f(z) = \log\Gamma\left(z\right)\) 32 Mb on disk, 440 Mb in RAM |
|
\(f(z) = \log\left(\Gamma\left(z\right)\right)\) 32 Mb on disk, 440 Mb in RAM |
|
\(f(z) = z^{3} + 3 \, z + \frac{1}{{\left(z - 2\right)}^{2}} + 8\) 90 Mb on disk, 1177 Mb in RAM |
|
34 Mb on disk, 460 Mb in RAM |
|
\(f(z) = e^{\left(i \, \sin\left(z\right)\right)}\) 69 Mb on disk, 910 Mb in RAM |
|
\(f(z) = e^{\left(\frac{5}{z^{4}}\right)}\) 99 Mb on disk, 1300 Mb in RAM |
|
\(f(z) = J_{0}(z) + i \, Y_{0}(z)\) 62 Mb on disk, 820 Mb in RAM |
|
22 Mb on disk, 310 Mb in RAM |
|
scaled by 50 times 76 Mb on disk, 980 Mb in RAM |
|
scaled by 2000 times 81 Mb on disk, 1050 Mb in RAM |
|
\(f(z) = 16 \, z^{5} - 20 \, z^{3} + 5 \, z\) 31 Mb on disk, 430 Mb in RAM |
|
\(f(z) = \operatorname{erf}\left(z\right)\) 49 Mb on disk, 640 Mb in RAM |
|
\(f(z) = \frac{\Gamma\left(z - i\right)^{2}}{\Gamma\left(z + i\right)^{2}}\) 73 Mb on disk, 940 Mb in RAM |
|
\(f(z) = \left(-i \, z\right)^{\frac{2}{3}} - \left(-z\right)^{\frac{2}{3}}\) 70 Mb on disk, 920 Mb in RAM |
|
where \(D_+(x) = \frac{\sqrt{\pi}}{2} e^{-x^{2}} \operatorname{erfi}\left(x\right)\) 44 Mb on disk, 590 Mb in RAM |
|
76 Mb on disk, 980 Mb in RAM |
|
54 Mb on disk, 710 Mb in RAM |
|
75 Mb on disk, 970 Mb in RAM |
|
80 Mb on disk, 1020 Mb in RAM |
|
81 Mb on disk, 1050 Mb in RAM |
|
80 Mb on disk, 1020 Mb in RAM |
|
81 Mb on disk, 1050 Mb in RAM |
|
81 Mb on disk, 1050 Mb in RAM |
|
81 Mb on disk, 1050 Mb in RAM |
|
\(f(z) = \log\left(K_{0}(z)\right)\) 68 Mb on disk, 880 Mb in RAM |
|
\(f(z) = \frac{\sin\left(z^{3} - 1\right)}{z}\) 44 Mb on disk, 630 Mb in RAM |
|
79 Mb on disk, 1140 Mb in RAM |
And now for something completely different
def p3d(f, *, nx=-2, px=2, ny=-2, py=2, D=1, is_log=False, top=3, hi_res=600): from matplotlib.cm import get_cmap cm = get_cmap("sheerluck") def _scale(x): if is_log: if x <= 0: return infinity return log(x) else: return x / D def _arg(x, y): val = f(x + I * y) # f(z) a = arg(val) + pi # f(z).arg τ = 2 * pi return n(a / τ) # [-π..π] -> [0..1] def _abs(x, y): val = f(x + I * y) # f(z) a = val.abs().n() # f(z).abs a = _scale(a) if a < top: return a return infinity def _real(x, y): val = f(x + I * y) # f(z) a = val.real().n() # f(z).real a = _scale(a) if -1 < a < top: return a - 0.03 return infinity P = plot3d( _abs, (x, nx, px), (y, ny, py), plot_points=hi_res, color=(_arg, cm)) Q = plot3d( _real, (x, nx, px), (y, ny, py), plot_points=hi_res, color="blue", opacity=0.5) return P + Q def thats_all_folks(): P = complex_plot( 1/x^2, (-9.5, 9.5), (-6.5, 6.5), ticks=[list(range(-10, 10)), list(range(-10, 10))], aspect_ratio=1, plot_points=700, contoured=True, figsize=11, cmap="Reds") Q = circle((0,0), 2.85, fill=True, rgbcolor=(0.0078, 0.1529, 0.2902)) return P + Q
see also https://trac.sagemath.org/ticket/33416